What Wikipedia’s Network Structure Can Tell Us About Culture

Wikipedia, like all websites, is structured as a network with links connecting one page to another. Each of Wikipedia’s almost 300 languages is written independently and thus may have different underlying network structures. What might we learn from these differences?
A Brief Introduction to Graph Theory
Those already familiar with graph theory can skip this section.
Graphs, in the mathematical sense, are structures that connect objects together with links. In Graph theory jargon, the objects are nodes and the links connecting them are edges. For example, in the graph below there are three nodes: A, B and C. A is connected to both B and C, but B is only connected to C through A.
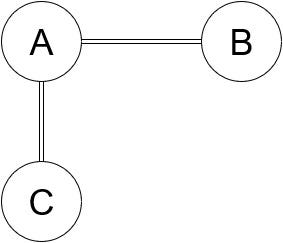
Edges can also be directional, signified by an arrow. For example, in the graph below you can travel from B to A, and C to A, but you can’t go anywhere from A itself.

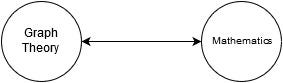
That’s really all there is to understanding basic graphs, but starting with just those fundamentals a lot of interesting work can be done. When modeling Wikipedia each article is a node and each link between articles is an edge. For example, the article on Graph Theory links to the article on Mathematics which links back to Graph Theory, represented by the two-headed arrow below.
Building the Wikipedia Graphs
The first step was collecting the network structure data for each language. Wikipedia is big — Almost 40 million pages today and when last calculated in 2009, 275 million links. Instead of working with the whole of Wikipedia, we wanted to get an “equal” sample of pages from each language. We did this by picking five pairs of city+language where the city is a major global city and the primary language spoken in that city is one of the largest Wikipedias. For each of these languages, we built a network using Wikipedia’s API by starting at all five cities, visiting all the pages linked to from that page and then visiting all the pages linked to from those pages.
The table below shows the five languages and cities as well as the number of nodes and edges in our sampled network for each of those languages. For comparison I’ve also included the total number of articles and the ratio to the total in our sample.
For each of the networks we did the following:
- Measured the centrality of each node. The centrality is a measure of how important a node is in a network. Importance of an article is based on how many articles link to that article and how important those articles are. This is the same method that Google uses to find the best search results.
- Detected communities of similar articles using modularity — essentially finding clusters of articles that are highly interconnected.
- Used Gephi to visualize the networks by coloring each node by the community it is in, and sizing the label by how important the node is.
Results
View the following images in all their giant glory here.

To start with, here is the graph for English. English appears the most “neutral” of any of the five languages, and that makes sense considering it is the biggest of the Wikipedias and is used all over the globe. I say “neutral” because it contains clusters for each of the countries where we started and is fairly circularly shaped, indicating interconnections even across communities.
The giant Eurovision Song Contest community is a first indication that “Wikipedia” important many not reflect actual cultural importance. The way the Eurovision Song Contest pages are written on Wikipedia leads to a lot of interlinking between them, which may overemphasize their importance. Not to discount the important cultural institution that is the Eurovision Song Contest…

Next, looking at Turkish, we see some differences. First, Turkey itself is more prominently in the center. This would make sense considering Turkish is not spoken widely outside of Turkey as opposed to English. We also see that Japan and China both just get lumped into a general Asia community. Neither New York nor the United States has any prominence. But the all important Eurovision community remains.

Turning to Russian, like Turkey in the Turkish network, here we see Russia prominently featured in the center. The most interesting feature here is the community in the top-left for New York. This happened because there are a large number of Wikipedia articles for tiny towns in New York that have only one edit and I can only assume were machine translated. Yet another way that Wikipedia won’t reflect reality.

The Japanese network is very similar in structure to the Russian one, including the odd New York State community. Interestingly, America (アメリカ合衆国) is about as central as Japan (日本).
Finally, looking at Chinese we see the most distinct of the five networks.

Instead of being round(ish) it’s elongated, indicating that there is not much interconnectivity between the two ends. In addition to a China community, we also see Shanghai getting it’s own distinct communities. And besides Russia, the rest of the world gets lumped into a single community.
What conclusions can we reasonably draw from this?
Does Japan have a greater fascination with America than with Turkey? Well, yes, probably. Are English speakers obsessed with Geographic Coordinate Systems? No, Wikipedia articles for places just usually include the latitude and longitude. Are Chinese speakers more culturally insular? Possibly, considering the Chinese government tries its hardest to make them so.
But it’s important to remember that the people (or machines) who write Wikipedia articles do not represent every speaker of their language. And, the structure and conventions of Wikipedia itself will emphasize some topics over others.
If nothing else, at least we got some pretty pictures.
Work done by Jeremy Neiman and Avigail Vantu as part of the masters program at New York University’s Center for Urban Science and Progress.
